222. 完全二叉树的节点个数 - 力扣（Leetcode）

给出一个完全二叉树，求出该树的节点个数。
完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

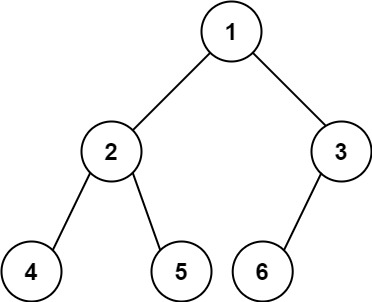
  • 输入：root = [1,2,3,4,5,6]
  • 输出：6

示例 2：

  • 输入：root = []
  • 输出：0

示例 3：

  • 输入：root = [1]
  • 输出：1

提示：

  • 树中节点的数目范围是[0, 5 * 10^4]
  • 0 <= Node.val <= 5 * 10^4
  • 题目数据保证输入的树是 完全二叉树

思路

  1. 使用普通二叉树的思想来求，使用层序遍历 或者递归
    增加一个变量来存node 的个数
  2. 利用完全二叉树的性质，他只有最后一层没有填满，并且是从左到右依次填满的。

代码实现

思路1：普通二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 递归
func countNodes(root *TreeNode) int {
    if root == nil {
        return 0
    }
    count := 1 //记录res, 递归算root=1
    if root.Right != nil {
        count += countNodes(root.Right)
    }
    if root.Left != nil {
        count += countNodes(root.Left)
    }
    return count
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 迭代
func countNodes(root *TreeNode) int {
    if root == nil {
        return 0
    }
    q := list.New()
    q.PushBack(root)
    res := 0 // 记录res, 这里root 加入到了队列，所以res=0 而不是1
    for q.Len() > 0 {
        n := q.Len()
        for i := 0; i < n; i++ {
            node := q.Remove(q.Front()).(*TreeNode)
            if node.Left != nil {
                q.PushBack(node.Left)
            }
            if node.Right != nil {
                q.PushBack(node.Right)
            }
            res++
        }
    }
    return res 
}

思路2：完全二叉树

  1. 确定递归函数的参数和返回值 ： 输入根节点，返回int 节点数
    1
    func countNodes(root *TreeNode) int {
  2. 递归终止条件，需要左右两边深度相同，则为满二叉树，调用 2^treeDepth - 1 计算node
  3. 单层递归逻辑：
    需要先求左子右树的节点数量（我们转化为满二叉树，使用公式计算）然后加上root
    结果等于 leftTreeNum + rightTreeNum + 1 （leftTreeNum为左子满二叉树，rightTreeNum为右子满二叉树，1是root）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func countNodes(root *TreeNode) int {
    if root == nil {
        return 0
    }
    
    leftH, rightH := 0, 0
    leftNode := root.Left
    rightNode := root.Right
    for leftNode != nil {
        leftNode = leftNode.Left
        leftH++
    }
    for rightNode != nil {
        rightNode = rightNode.Right
        rightH++
    }
    // 递归终止条件，需要左右两边深度相同，则为满二叉树，调用 2^treeDepth - 1 计算node
    if leftH == rightH {
        return (2 << leftH) - 1  // 2左移 即为平方
    }
    leftTreeNum := countNodes(root.Left) // 左
    rightTreeNum := countNodes(root.Right) // 右
    res := leftTreeNum + rightTreeNum + 1 // 中
    return res
}