leetcode 2594修车的最少时间

2594. 修车的最少时间 - 力扣（LeetCode）

思路

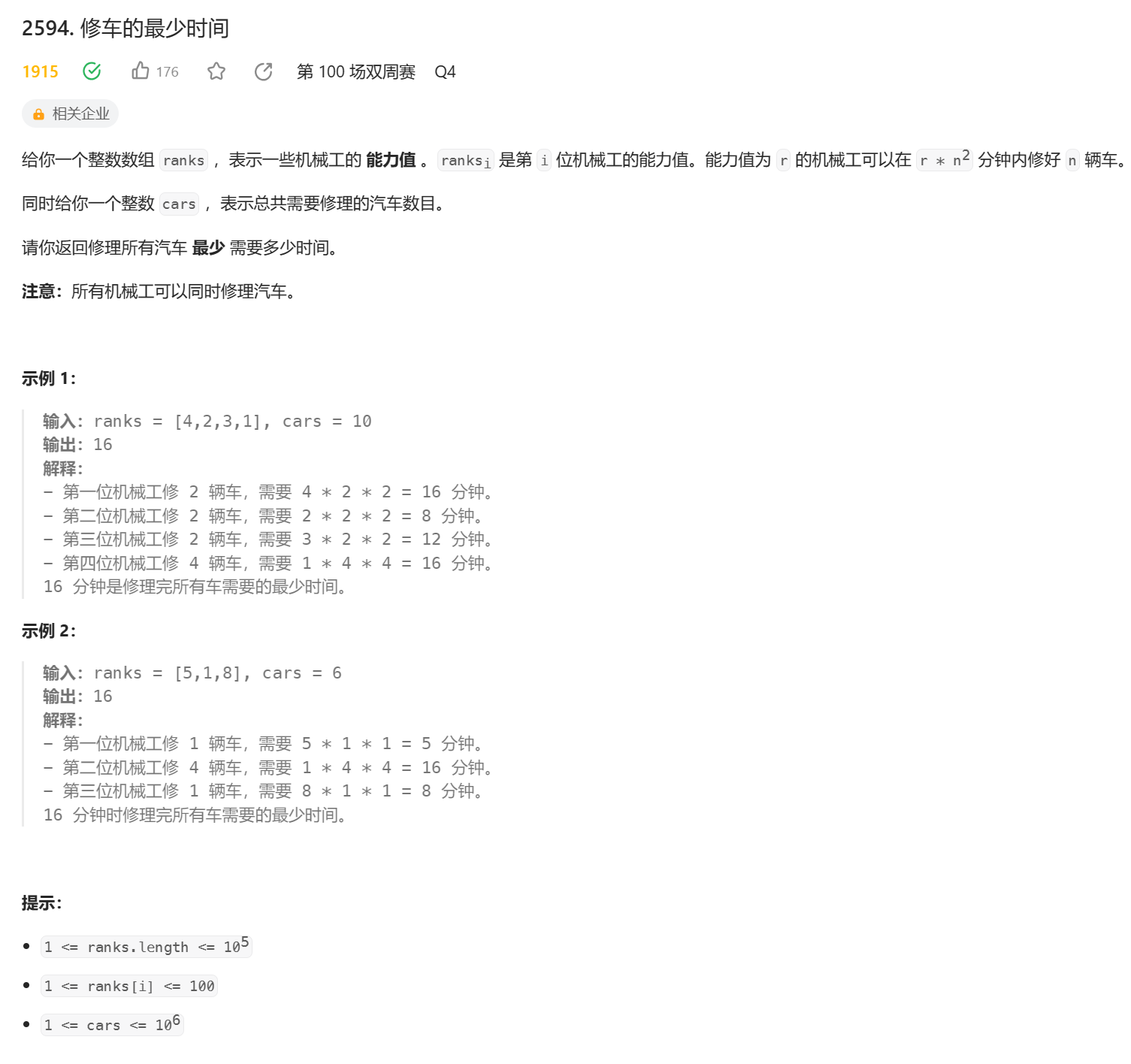
能力值为 r 的机械工可以在 t= r * n2 分钟内修好 n 辆车。
可以看到 n = 根号(t/r), t 对于car 的数量是单调增的，所以可以适用二分法来不断逼近car 的数量。

func repairCars(ranks []int, cars int) int64 {
    l , r := 1, ranks[0] * cars * cars
    var check = func(m int) bool {
        cnt := 0
        for _, x := range ranks {
            cnt += int(math.Sqrt(float64(m / x)))
        }
        return cnt >= cars
    }
        
    for l < r {
        m := (l + r) >> 1
        if check(m) {
            r = m
        } else {
            l = m + 1
        }
    }
    return int64(l)
}

1. l 和 r 的初始化：

   • l 初始化为1，表示最小可能的修理时间。
   • r 初始化为 ranks[0] * cars * cars，表示最大可能的修理时间。这里假设第一个机械工的能力值最高，所以最大时间是他修理所有汽车所需的时间。

2. check 函数定义：

   • 这个函数用于检查给定的修理时间是否足够，以修理所有汽车。它接受一个整数 m 作为参数，表示修理时间。然后，它遍历每个机械工的能力值，计算每个机械工在 m 时间内能修理多少辆车，然后累加到 cnt 变量中。
   • 如果 cnt 大于或等于需要修理的汽车数量 cars，则返回 true，否则返回 false。

3. 二分查找循环：

   • 使用一个二分查找循环来查找最小的修理时间。循环条件是 l < r，即当最小时间小于最大时间时，继续循环。
   • 在每次循环中，计算中间值 m，并调用 check(m) 检查是否满足修理所有汽车的条件。
   • 如果满足条件，则将 r 更新为 m，因为我们希望找到更小的修理时间。
   • 如果不满足条件，则将 l 更新为 m + 1，因为我们需要增加修理时间。
   • 这样，不断地缩小时间范围，直到找到最小的修理时间。

4. 最终返回结果：

   • 一旦 l 不再小于 r，循环结束，说明已经找到了最小的修理时间，将其转换为 int64 类型并返回。

我们总结一下二分查找适用的场景

二分查找算法适用场景

递增或递减规律：数据集合必须遵循某种递增或递减的规律，以确保二分查找的有效性。二分查找前提就是单调的。

有序数据集合：二分查找要求数据集合必须是有序的，无论是升序还是降序都可以。

快速查找：对于大型数据集，二分查找是一种高效的查找算法，因为它每次都将数据集合减半。

确定性问题：二分查找通常用于解决确定性问题，即要么找到目标，要么确定目标不存在。它不适用于涉及模糊匹配或多个匹配项的情况。

时间复杂度要求较高：在需要快速找到目标的情况下，二分查找的时间复杂度为O(log n)，对于大规模数据集非常高效。

可比较性数据：二分查找要求能够比较数据元素的大小，因此适用于数字、字符等可比较的数据类型。

搜索范围可确定：二分查找适用于可以确定搜索范围的问题，通常通过定义一个左边界和右边界来实现。

内存连续性：在一些需要高效的内存访问场景中，二分查找比线性搜索更有效，因为它充分利用了内存的连续性。

一些具体的应用场景包括在有序数组中查找元素、查找某个值的边界、查找某个值的插入位置、查找满足某个条件的最大或最小值等。