739. 每日温度 - 力扣（LeetCode）


栈里边存放的是还没有找到后边更大值的元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 从左向右，
func dailyTemperatures(temperatures []int) []int {
    length := len(temperatures)  // 长度 
    ans := make([]int, length)   // 返回的数组
    stack := []int{}            // 单调栈
    for i := 0; i < length; i ++ {
        temperature := temperatures[i] 
        fmt.Println("temperature:", temperature)
        fmt.Println("stack:", stack)
        for len(stack) > 0 && temperature > temperatures[stack[len(stack) -1]] {
            fmt.Println("temperature now:", temperature, temperatures[stack[len(stack) -1]], stack[len(stack) -1])
            preindex := stack[len(stack)-1] // 上一个位置的index
            stack = stack[:len(stack) -1] // 栈顶找到了当前更大的数，
            ans[preindex] = i -preindex // 记录位置
        }
        stack = append(stack, i) // 如果不满足要求，则说明是小的数，需要添加到栈中
    }
    return ans
}


// 从右向左

func dailyTemperatures(temperatures []int) []int {
    lens := len(temperatures)
    ans := make([]int, lens)
    stack := []int{}  // 单调递增栈（从栈底到栈顶）
    
    for i := lens-1; i >= 0; i-- {
        temperature := temperatures[i]
        // 弹出所有小于等于当前温度的索引
        for len(stack) > 0 && temperature >= temperatures[stack[len(stack)-1]] {
            stack = stack[:len(stack)-1]
        }
        // 如果栈不为空，栈顶就是第一个比当前大的温度
        if len(stack) > 0 {
            ans[i] = stack[len(stack)-1] - i
        }
        stack = append(stack, i)
    }
    return ans
}




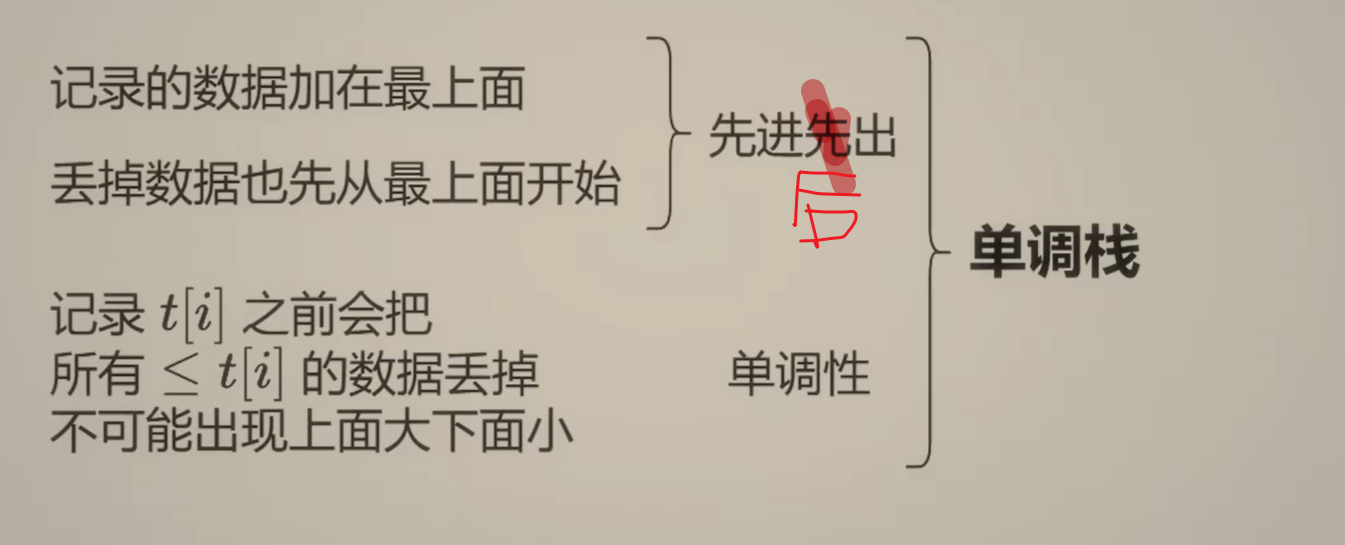
单调栈 适用于 上一个更大(更小)元素，或者下一个更大（小）元素

这段代码是一个Go语言编写的函数，名为dailyTemperatures，它使用单调栈的数据结构来解决一个特定问题：给定一个每日温度列表temperatures，返回一个新列表，其中第i个元素是温度列表中第i天之后第一个比第i天温度更高的温度的天数。

代码思想解释：

  1. 问题定义：我们想要找到一个序列中每个元素之后的第一个更大元素，并记录它们之间的索引差。

  2. 单调栈的应用：单调栈是一种特殊的栈结构，它保证栈内的元素是单调递增或单调递减的。在这个场景中，我们使用单调栈来维护一个索引栈，栈内元素代表尚未找到更大温度的天的索引。

  3. 初始化：

    • n：记录输入温度数组的长度。
    • ans：初始化一个长度为n的数组，用于存储结果，初始值设为0。
    • st：初始化一个空的切片，用作单调栈。

  4. 遍历温度数组：

    • 通过range关键字遍历temperatures数组，同时获取索引i和对应的温度值t。

  5. 维护单调栈：

    • 当前温度t大于栈顶元素对应的温度时，说明栈顶元素之后的第一个更高温度就是当前温度。此时，执行以下操作：
      • 弹出栈顶元素j，即st[len(st)-1]。
      • 计算索引差i - j，并将这个差值赋给ans[j]。
      • 更新栈st，移除栈顶元素。

  6. 压栈操作：

    • 将当前索引i压入栈st中。这表示当前索引的天还没有找到之后的第一个更高温度。

  7. 返回结果：

    • 遍历结束后，返回ans数组，其中每个元素表示对应天之后第一个更高温度的天数。

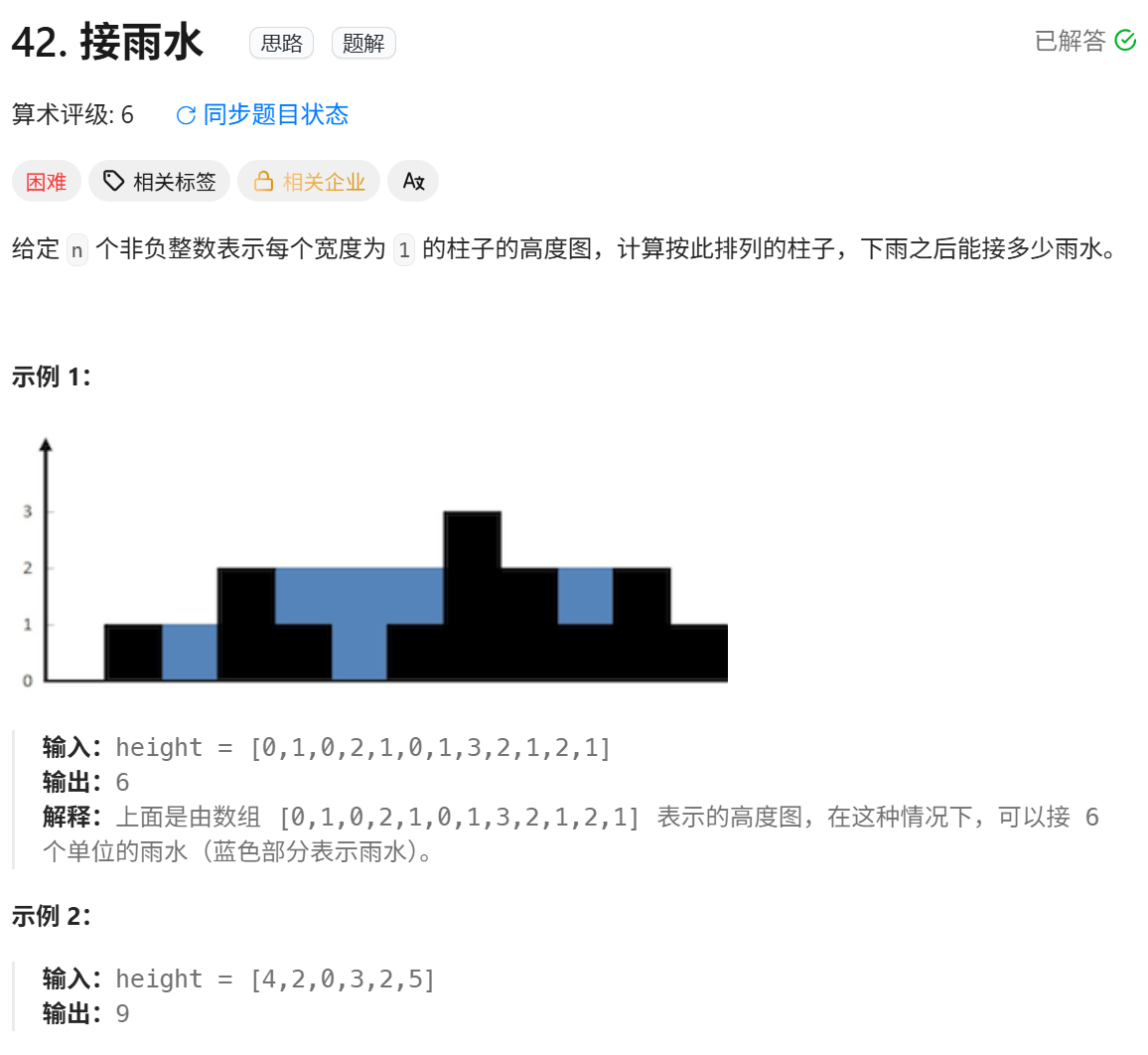
接雨水

42. 接雨水 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

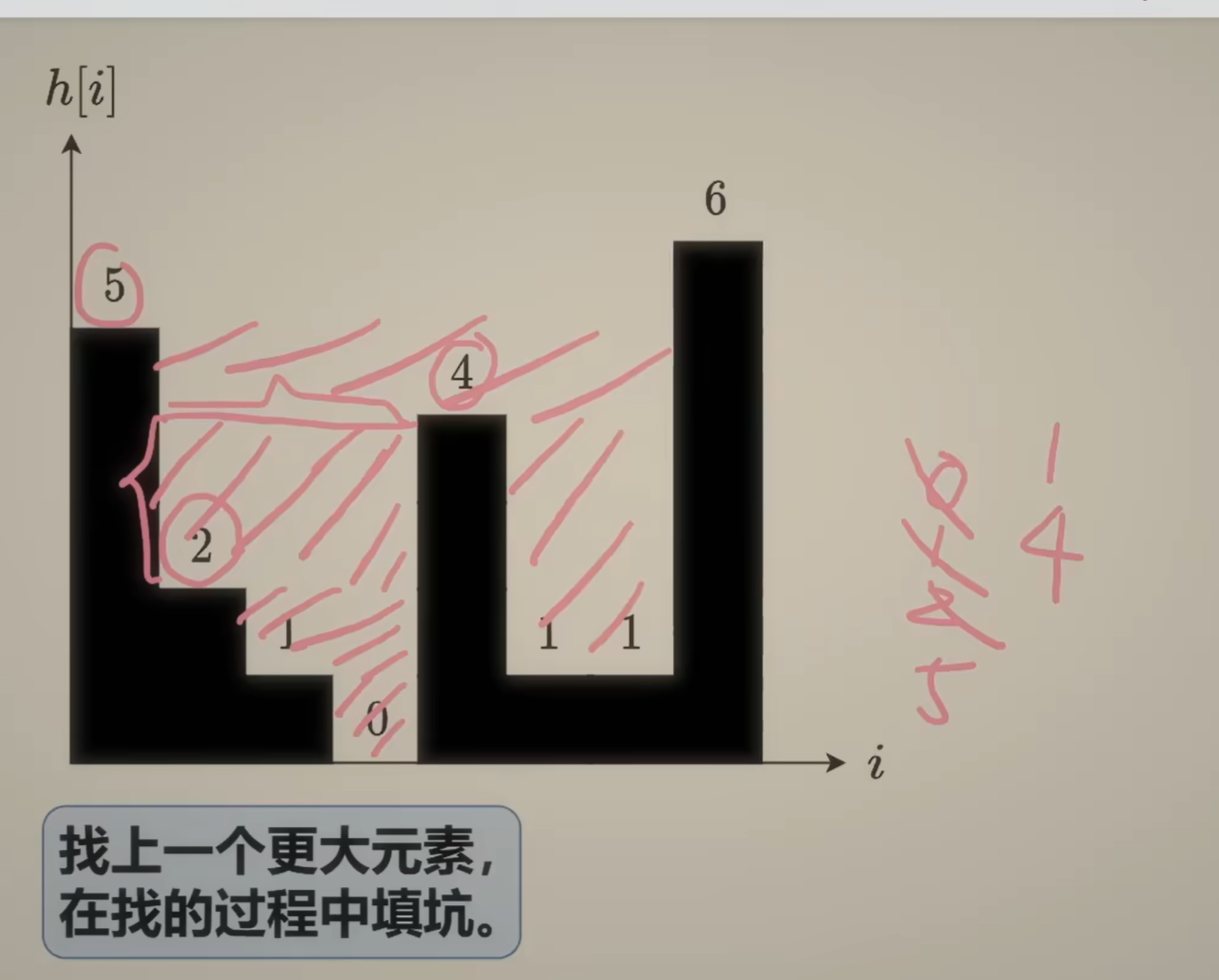
func trap(height []int) (ans int) {
    st := []int{}
    for i, h := range height {
        for len(st) > 0 && h >= height[st[len(st)-1]] { // 1. **处理相等高度的情况**：
%%     
    - 当遇到相等高度的柱子时，后面的柱子才是有效的右边界
        
    - 使用`>=`可以正确处理这种情况，确保弹出所有小于等于当前高度的柱子
        
    - 如果只用`>`，相等高度的柱子会留在栈中，导致计算错误 %%
            bottomH := height[st[len(st)-1]]
            st = st[:len(st)-1]
            if len(st) == 0 {
                break
            }
            left := st[len(st)-1]
            dh := min(height[left], h) - bottomH // 面积的高
            ans += dh * (i - left - 1)// 面积高*宽
        }
        st = append(st, i)
    }
    return
}

## 示例分析

以高度数组`[0,1,0,2,1,0,1,3,2,1,2,1]`为例：

1. 遇到第二个高度为1的柱子时：
    
    - 弹出之前高度为0的柱子
        
    - 计算它与左边高度1的柱子之间的雨水
        
2. 遇到高度为2的柱子时：
    
    - 弹出高度为1的柱子（因为2 >= 1）
        
    - 计算它与左边更高柱子之间的雨水
        
3. 遇到相等高度1的柱子时：
    
    - 前面的1被弹出（因为1 >= 1）
        
    - 确保新的1作为右边界参与后续计算

单调队列

239. 滑动窗口最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

func maxSlidingWindow(nums []int, k int) []int {
    ans := make([]int, 0, len(nums)-k+1) // 预分配空间
    q := []int{}
    for i, x := range nums {
        // 1. 入
        for len(q) > 0 && x >= nums[q[len(q)-1]] {
            q = q[:len(q)-1] // 维护 q 的单调性 从大到小
        }
        q = append(q, i)

        // 2. 出
        if q[0] <= i -k{ // 队首已经离开窗口了
            q = q[1:] // Go 的切片是 O(1) 的
        }

        // 3. 记录答案
        if i >= k-1 {
            // 由于队首到队尾单调递减，所以窗口最大值就是队首
            ans = append(ans, nums[q[0]])
        }
    }
    return ans
}

从「维护单调性」的角度上来说，单调队列和单调栈是一样的，一个弹出队尾元素，另一个弹出栈顶元素。在单调栈的基础上，单调队列多了一个「移除队首」的操作，这类似滑动窗口移动左指针 left 的过程。所以从某种程度上来说，单调队列 = 单调栈 + 滑动窗口。