子集型回溯

17. 电话号码的字母组合 - 力扣（LeetCode）



方法一：输入的视角（选或不选）
对于输入的 nums，考虑每个 nums[i] 是选还是不选，由此组合出 2
n
个不同的子集。

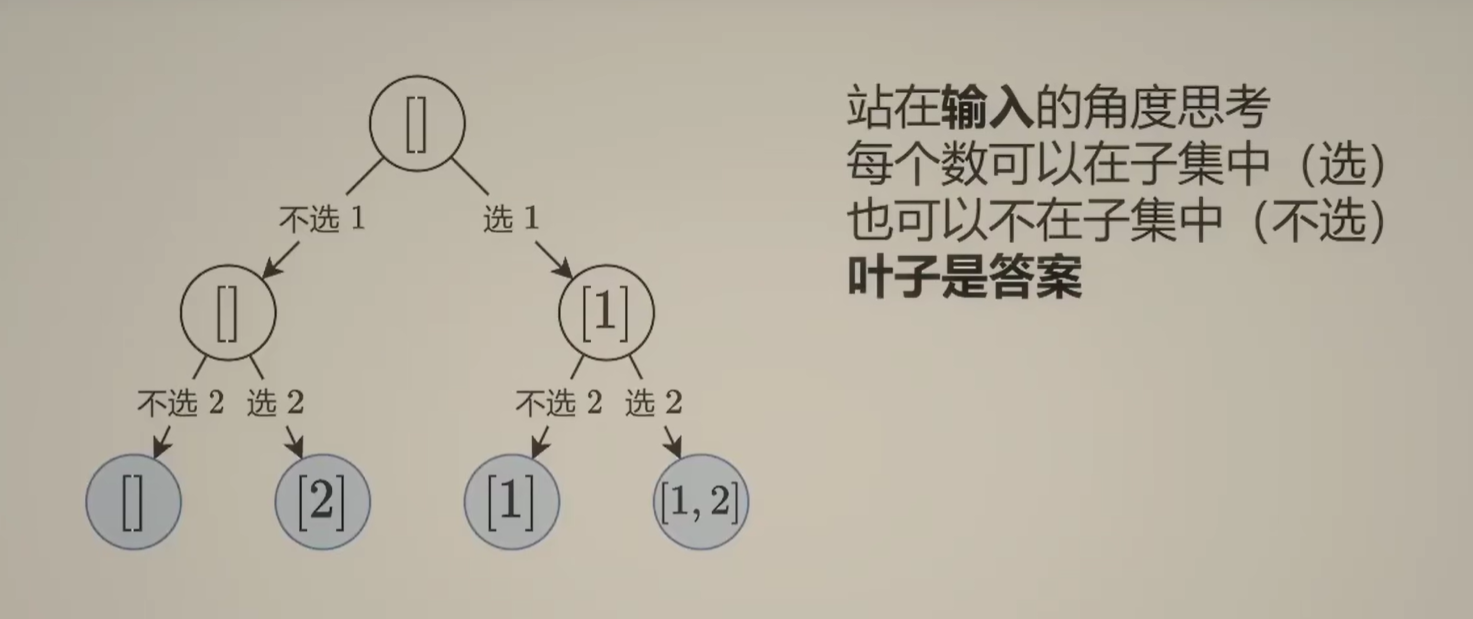
dfs 中的 i 表示当前考虑到 nums[i] 选或不选。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func subsets(nums []int) [][]int {
    n := len(nums)
    ans := make([][]int, 0, 1<<n) // 预分配空间
    path := make([]int, 0, n) // 预分配空间
    var dfs func(int)
    dfs = func(i int) {
        if i == n { // 子集构造完毕
            ans = append(ans, slices.Clone(path)) // 复制 path
            return
        }
        
        // 不选 nums[i]
        dfs(i + 1)
        
        // 选 nums[i]
        path = append(path, nums[i])
        dfs(i + 1)
        path = path[:len(path)-1] // 恢复现场
    }
    dfs(0)
    return ans
}

方法二：答案的视角（枚举选哪个）
枚举子集（答案）的第一个数选谁，第二个数选谁，第三个数选谁，依此类推。

dfs 中的 i 表示现在要枚举选 nums[i] 到 nums[n−1] 中的一个数，添加到 path 末尾。

如果选 nums[j] 添加到 path 末尾，那么下一个要添加到 path 末尾的数，就要在 nums[j+1] 到 nums[n−1] 中枚举了。

注意：不需要在回溯中判断 i=n 的边界情况，因为此时不会进入循环，if i == n: return 这句话写不写都一样.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
func subsets(nums []int) [][]int {
    n := len(nums)
    ans := make([][]int, 0, 1<<n) // 预分配空间
    path := make([]int, 0, n) // 预分配空间
    var dfs func(int)
    dfs = func(i int) {
		if i == n {
			return
		}
        for j := i; j < n; j++ { // 从当前索引向后枚举
            path = append(path, nums[j])  // 选择数字
            dfs(j + 1)                   // 递归下一层
            path = path[:len(path)-1]     // 回溯
        }
        // 关键位置：在递归开始时记录当前路径
        ans = append(ans, slices.Clone(path))
    }
    dfs(0)
    return ans
}


func subsets(nums []int) [][]int {
    n := len(nums)
    ans := make([][]int, 0, 1<<n) // 预分配空间
    path := make([]int, 0, n) // 预分配空间
    var dfs func(int)
    dfs = func(i int) {
		if i == n {
			return
		}
        // 关键位置：在递归开始时记录当前路径
        ans = append(ans, slices.Clone(path))
        for j := i; j < n; j++ { // 从当前索引向后枚举
            path = append(path, nums[j])  // 选择数字
            dfs(j + 1)                   // 递归下一层
            path = path[:len(path)-1]     // 回溯
        }
    }
    dfs(0)
    return ans
}

  1. 分割回文串 https://leetcode.cn/problems/palindrome-partitioning/solutions/2059414/hui-su-bu-hui-xie-tao-lu-zai-ci-pythonja-fues/

从答案的角度，枚举选哪个，需要使用for循环：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
func isPalindrome(s string, left, right int) bool {
    for i, j := left, right;i < j; i, j = i+1, j-1 {
        if s[i] != s[j] {
            return false
        }
    }
    return true
}

func partition(s string) (ans [][]string) {
    n := len(s)
    path := []string{}

    // 考虑 s[i:] 怎么分割
    var dfs func(int)
    dfs = func(i int) {
        if i == n { // s 分割完毕
            ans = append(ans, slices.Clone(path))
            return
        }
        for j := i; j < n; j++ { // 枚举子串的结束位置
            if isPalindrome(s, i, j) {
                path = append(path, s[i:j+1]) // 分割！
                // 考虑剩余的 s[j+1:] 怎么分割
                dfs(j + 1)
                path = path[:len(path)-1] // 恢复现场
            }
        }
    }

    dfs(0)
    return
}
  1. 电话号码的字母组合 https://leetcode.cn/problems/letter-combinations-of-a-phone-number/solutions/2059416/hui-su-bu-hui-xie-tao-lu-zai-ci-pythonja-3orv/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
var (
    m []string
    path []byte
    res []string
)

func letterCombinations(digits string) []string {
	// 将index 和 字符串对应起来
	m = []string{"","","abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}
	path, res = make([]byte,0),make([]string,0)
    if digits == "" {
        return res
    }
	backTracking(digits,0)
	return res
}
func backTracking(digits string, start int) {
	// 终止条件 ，遍历完digits
	if start == len(digits) {
        tmp := string(path)
		res = append(res,tmp)
		return
	}
	// 找到 digit
	digitNum := int(digits[start] - '0')
	// 遍历 digit 对应的map 字符串
	str := m[digitNum]
	for i:=0;i< len(str);i++ { // i 从0开始，因为每个字典都是一个独立的集合，之前的组合是一个集合，所以才从start 开始
		path = append(path,str[i])
		backTracking(digits,start+1)
		path =path[:len(path)-1]
	}
}

组合型回溯

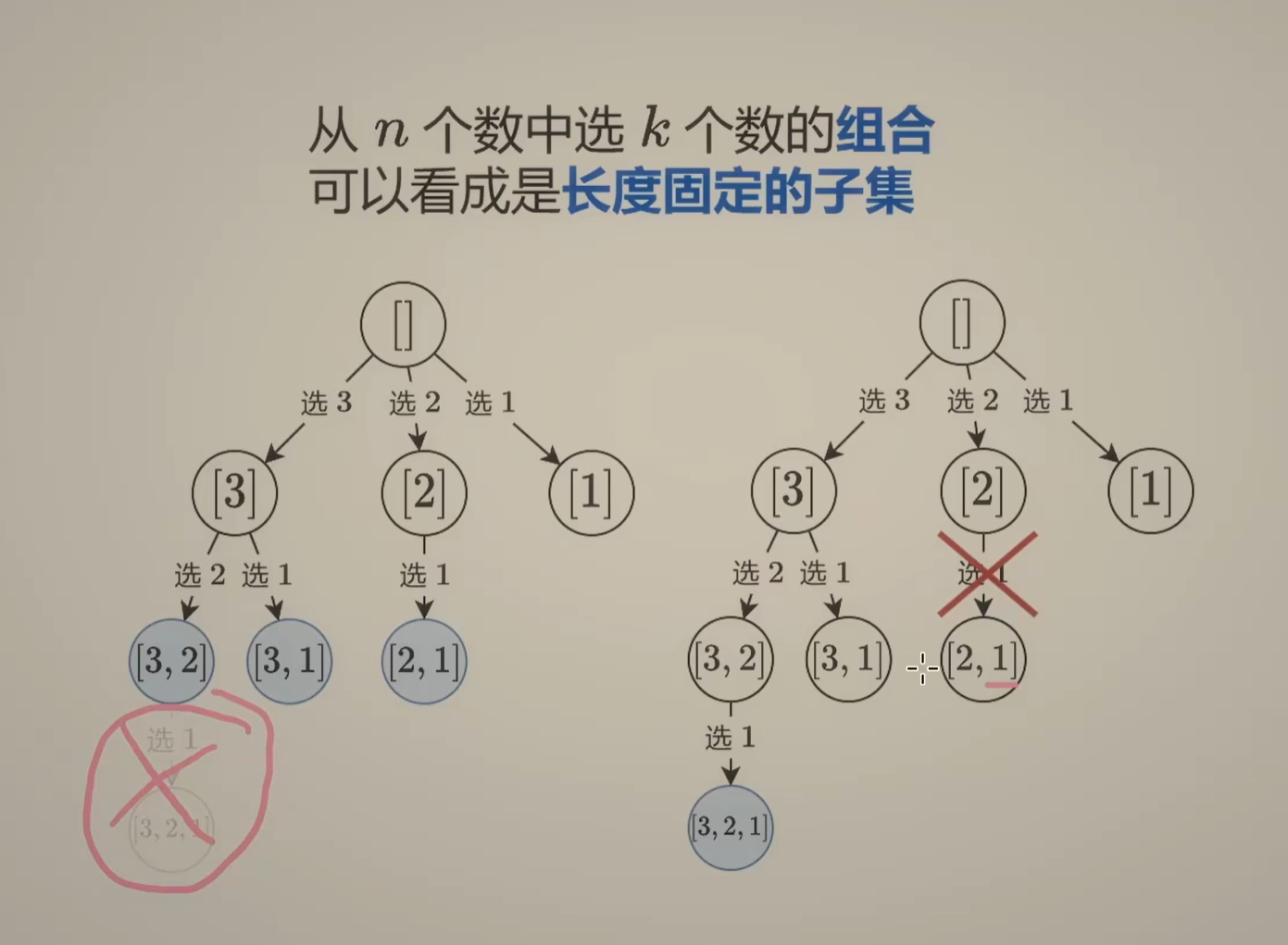
  1. 左边选或者不选 K=3 右边k = 2, 因为是组合，等于是重复的就能再出现了，再选了2 之后，只能选1 了， 不能再选其他的了。

    倒序的不等式简单点，正序的不等式为 n - i + 1 < d 直接return

77. 组合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
// 倒序遍历减枝
func combine(n int, k int) [][]int {
	// 组合
	if k > n {
		return [][]int{}
	}
	res := [][]int{}
	path := []int{}
	var dfs func(start int) // 下一个位置的组合
	dfs = func(start int) {
		// base case
		if len(path) == k {
			tmp := make([]int, k)
			copy(tmp, path) // copy 目标值在前边
			res = append(res, tmp)
		}

		for i := start; i >= 1; i-- {
			//path 还需要 k - len(path) 提前减枝
			if i < k-len(path) { // 注意是k - len(path)
				break
			}

			path = append(path, i)
			dfs(i - 1)
			path = path[:len(path)-1]
		}
	}
	dfs(n)
	return res
}

// 正序遍历减枝
func combine(n int, k int) [][]int {
	// 组合
	if k > n {
		return [][]int{}
	}
	res := [][]int{}
	path := []int{}
	var dfs func(start int) // 下一个位置的组合
	dfs = func(start int) {
		// base case
		if len(path) == k {
			tmp := make([]int, k)
			copy(tmp, path) // copy 目标值在前边
			res = append(res, tmp)
		}

		for i := start; i <= n; i++ { // 倒序方便
			//path 还需要 k - len(path) 提前减枝
			if n-i+1 < k-len(path) { // 注意是k - len(path)
				break
			}

			path = append(path, i)
			dfs(i + 1)
			path = path[:len(path)-1]
		}
	}
	dfs(1)
	return res
}


组合3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
package leetcode216

func combinationSum3(k int, n int) [][]int {
	res := [][]int{}
	path := []int{}

	var dfs func(start, sum int)
	dfs = func(start, sum int) {

		// 找到一个合法组合
		if len(path) == k && sum == n {
			tmp := make([]int, k)
			copy(tmp, path)
			res = append(res, tmp)
			return
		}

		// 剪枝：剩余数字不足以填满 path 或无法达到 sum
		for i := start; i >= 1; i-- {
			if i < k-len(path) { // 确保剩余数字足够填满 path
				break
			}
			if sum+i > n { // 提前终止，避免无效递归  如果 sum + i > n，说明当前 i 太大，不能选它。但 更小的 i 仍然可能满足 sum + i <= n，所以不能直接 break（否则会漏掉可能的解）。
				continue
			}
			path = append(path, i)
			dfs(i-1, sum+i)
			path = path[:len(path)-1]
		}
	}

	dfs(9, 0) // 数字范围是 1~9
	return res
}

22. 括号生成

思路题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
// 动态数据 回退操作

import "strings"

func generateParenthesis(n int) []string {
	//n 对括号 只要最后左右总和一样，
	m := n * 2
	res := []string{}

	var dfs func(i, open int)
	path := []string{}
	dfs = func(i, open int) {
		if i == m {
			res = append(res, strings.Join(path, ""))
		}

		// 选左边
		if open < n {
			path = append(path, "(")
			dfs(i+1, open+1)
            path = path[:len(path)-1]
		}

		// 选右边
		if i-open < open { // 右边要小于左边才能加
			path = append(path, ")")
			dfs(i+1, open)
            path = path[:len(path)-1]
		}

	}
    dfs(0, 0) // 入口函数需要添加
	return res
}


// 固定长度+索引，不用回退
func generateParenthesis(n int) (ans []string) {
    m := n * 2
    path := make([]byte, m)
    var dfs func(int, int)
    dfs = func(i, open int) {
        if i == m {
            ans = append(ans, string(path))
            return
        }
        if open < n { // 可以填左括号
            path[i] = '('
            dfs(i+1, open+1)
        }
        if i-open < open { // 可以填右括号
            path[i] = ')'
            dfs(i+1, open)
        }
    }
    dfs(0, 0)
    return
}

在你提供的这个实现中，不需要显式的回退操作（如 path = path[:len(path)-1]），是因为它采用了 固定长度的 []byte 数组 和 索引覆盖 的方式，这与常见的回溯算法实现有所不同。下面详细解释为什么可以省略回退操作：

关键原因分析

1. 使用固定长度的 []byte 数组

1
path := make([]byte, m)  // 长度为 m 的固定数组
  • 数组 path 的长度在初始化时就固定为 m（=n*2），不会动态增长。
  • 每个递归层级直接通过索引 i 修改 path[i] 的位置，不会影响其他层级的存储。

2. 索引覆盖写入

1
path[i] = '('  // 或 path[i] = ')'
  • 每次写入都会精确覆盖 path[i] 的位置，而不会追加元素。
  • 递归返回时，上层调用会覆盖当前层写入的值，因此不需要手动回退。

3. 递归的自然回溯

  • 当递归从深层返回时，上层调用会继续修改 path 的后续位置，覆盖之前的值。
  • 例如：
    • 第一层递归写入 path[0] = '('，然后进入第二层。
    • 第二层写入 path[1] = '(' 或 path[1] = ')'。
    • 当第二层递归返回后，第一层可能会写入 path[1] = ')'，覆盖之前的值。

对比需要回退操作的实现

需要回退的版本（动态 append）

1
2
3
4
path := []string{}
path = append(path, "(")  // 修改切片长度
dfs(...)
path = path[:len(path)-1] // 必须回退
  • 动态 append 会改变切片长度，必须显式回退以恢复状态。

不需要回退的版本（固定数组 + 索引覆盖）

1
2
3
4
path := make([]byte, m)
path[i] = '('  // 直接覆盖，不改变长度
dfs(...)
// 无需回退，上层调用会覆盖 path[i]
  • 固定数组的长度不变，通过索引直接修改值，递归返回后自然被覆盖。

为什么这种写法是正确的？

  1. 隐式回溯：

    • 每一层递归的 path[i] 写入是独立的，递归返回后会被上层调用覆盖。
    • 例如：
      • 路径 "(())" 的生成过程：
        1
        2
        3
        4
        path[0] = '('  // 第一层
        path[1] = '('  // 第二层
        path[2] = ')'  // 第三层
        path[3] = ')'  // 第四层
      • 如果第二层尝试 path[1] = ')'，它会覆盖之前的 '('，但通过条件 i-open < open 保证了合法性。

  2. 条件保证合法性：

    • open < n 确保左括号不超过 n 个。
    • i-open < open 确保右括号数不超过左括号数。
  • 不需要回退：因为使用了固定长度的 []byte 数组，通过索引直接覆盖写入，递归返回时上层调用会自然覆盖当前层的修改。
  • 更高效：避免了动态切片的扩容和回退操作，减少了内存分配。
  • 更简洁：代码更紧凑，但需要理解索引覆盖的隐式回溯逻辑。

这种写法是回溯算法的一种优化技巧，适用于结果长度固定的场景（如括号生成、排列问题等）。

排列型回溯