leetcode 最大深度和最小深度

题目

104. 二叉树的最大深度 - 力扣（LeetCode）

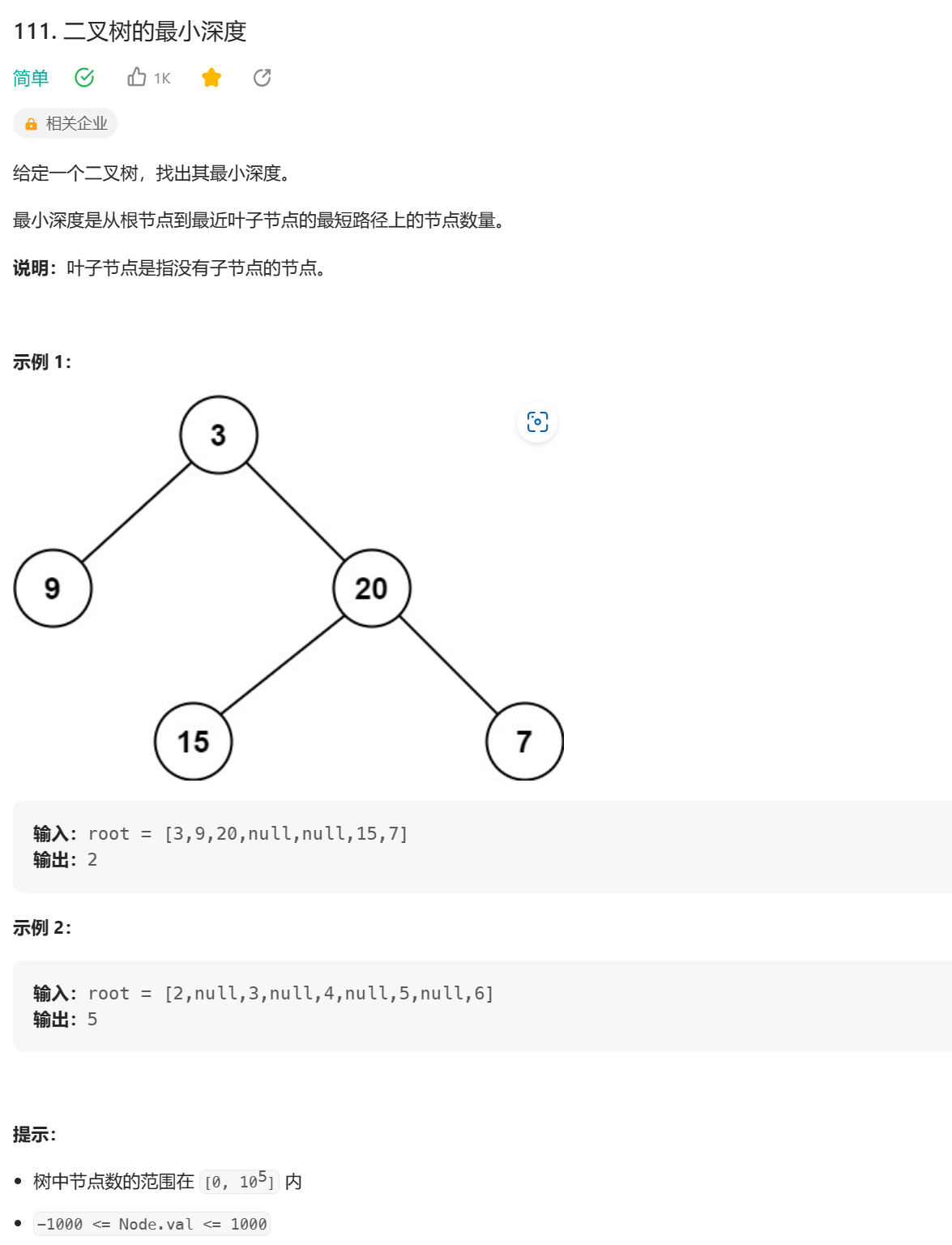
111. 二叉树的最小深度 - 力扣（LeetCode）

思路

深度 是指从根节点到该节点的距离（节点数量）
高度 是指从该节点到叶子节点的角力（节点数量）

最大深度 可以通过迭代法，计算总共有多少层。 可以使用递归分治的思想，1 + maxDepth(左子树) + maxDepth(右子树)
最小子树 其实和最大深度类似，但是这里要注意的是，不能直接套用最大深度的代码。最小子树的要求是，到叶子节点的距离。而上边最大深度没有这个要求。所以要对一侧子树为空的情况需要单独讨论。以下是代码实现：

最大深度

递归分治

后序遍历 需要调用自生函数，需要严格按照定义调用递归。

// 定义：输入根节点，返回这棵二叉树的最大深度
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    rightMaxDepth := maxDepth(root.Right)
    leftMaxDepth := maxDepth(root.Left)
    return 1 + max(rightMaxDepth,leftMaxDepth)
}

func max(a,b int) int {
    if a > b {
        return a
    }
    return b
}

迭代 层序遍历

// 定义：输入根节点，返回这棵二叉树的最大深度
func maxDepth(root *TreeNode) int {
	depth := 0;
    if root == nil {
        return 0
    }
	queue := []*TreeNode{}

	queue = append(queue,root)
	for len(queue) > 0 { // queue 不为空的时候
		size := len(queue)
		for i:=0;i <size ;i++ {// 遍历一层
			top := queue[0]
			queue = queue[1:] // 取最上层元素，并切掉该元素
			if top.Right != nil {
				queue = append(queue,top.Right)
			}
			if top.Left != nil {
				queue = append(queue,top.Left)
			}
		}
        depth++
	}
	return depth
}

最小深度

递归

后序遍历

// 定义：输入根节点，返回这棵二叉树的最小深度

func minDepth(root *TreeNode) int {

    if root == nil {
        return 0
    }
    rightMaxDepth := minDepth(root.Right)

    leftMaxDepth := minDepth(root.Left)

    // 注意 最小深度是要到叶子节点的距离，对于一侧子树为空的情况需要单独讨论

    if root.Right == nil && root.Left !=nil {
        return 1 + leftMaxDepth // 注意前面已经计算了rightMin 后边就直接调用这个函数， 不要再写个递归函数，否则会超时。
    }
    if root.Left == nil && root.Right !=nil {
        return 1 + rightMaxDepth
    }
    return 1 + min(rightMaxDepth,leftMaxDepth)

}

  
func min(a,b int) int {
    if a > b {
        return b
    }
    return a
}

迭代 层序遍历

func minDepth(root *TreeNode) int {
	depth := 0;
	
    if root == nil {
        return 0
    }
	queue := []*TreeNode{}
	
	queue = append(queue,root)
	for len(queue) > 0 { // queue 不为空的时候
		size := len(queue)
		for i:=0;i <size ;i++ {// 遍历一层
			top := queue[0]
			queue = queue[1:] // 取最上层元素，并切掉该元素
			if top.Right != nil {
				queue = append(queue,top.Right)
			}
			if top.Left != nil {
				queue = append(queue,top.Left)
			}
			
			if top.Right == nil && top.Left == nil {
				return depth + 1 // 当前节点也算哦
			}
		}
        depth++
	}
	return depth
}